Страница 5 из 39
Разработка Gcodetools - плагин Inkscape для экспорта в Gкод
Добавлено: 07 дек 2009, 11:39
Nick
Разработка Gcodetools
Эта ветка посвящена разработке
Gcodetools, плагина для векторного редактора
Inkscape, позволяющего конвертировать кривые из Inkscape в Gкод, используя круговую и линейную интерполяцию.
Описание работы, установка, помошь и уроки по плагину можно найти в теме:
Gcodetools - plug-in Inkscape для экспорта в Gcode
На данный момент ведется работа над Gcodetools 1.7
Что мы хотим увидеть в новой версии:
- Улучшение расширения для плазменной резки
- Добавление дополнительных опций экспорта:
- Улучшение функции обработки площади
- Угол заглубления
- Расширение для сверловки
Требуются
- Тестеры
- Разработчики
- Помощь в технических аспектах по работе станков и обработке материалов
- Новые идеи
Последняя версия
Исходный код находится на launchpad.net. Получить последнюю версию при помощи bazaar можно так:
Последнюю версию можно загрузить через web-интерфейс:
http://bazaar.launchpad.net/~gcodetools ... lope/files
Установка
1. Загрузите последнюю ревизию, из указанных выше мест.
2. Выполните "python create_inx.py" в директории с загруженными файлами.
3. Скопируйте все созданные файлы с расширением *.inx и файл gcodetools-dev.py в каталог:
Linux: /usr/share/inkscape/extensions/ и перезапустите inkscape
Windows: Program Files\Inkscape\share\extensions\
4. Перезапустите Inkscape
Последняя версия может быть не рабочей! Для получения стабильной рабочей версии зайдите сюда
Gcodetools - plug-in Inkscape для экспорта в Gcode или загрузите предыдущие ревизии.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 20:28
Nick
Dormouse, Под виндой все работает, только что проверил с версией из шапки.
Если не сложно, напиши маленький баг репорт:
1. Файл который выдает ошибку.
2. Скрин или копия сообщения об ошибке.
3. Скрин настроек.
Очень странно, что на header и footer ругается

, не должен.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 12:12
Nick
Вычислил вчера все частные производные этой системы, получилось всего на страничку

.
Я тут подумал, и понял, что когда мы решаем эту систему численно, то фактически прикладываем окружность в какой-то точке и пытаемся сместить ее, чтобы улучшить результат. Разница лишь в том, что для решения используется метод Ньютона, который гарантирует сходимость причем достаточно быструю

.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 12:41
Nick
Блин... Забыл расчет производной дома

. Начал вычислять заново и понял, что ошибся с изначальной системой (хорошо что сейчас обнаружил

).
Система должна быть такая:

Код: Выделить всё
alignl {
left lbrace alignl stack{
x = x_1+t_1 n_x1#y = y_1+t_1 n_y1
} right none
} newline newline
alignl {
left lbrace alignl stack{
x = x_2+t_2 n_x2#
y = y_2+t_2 n_y2#
x_2 = a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x#
y_2 = a_y t_{3}^3 + b_y t_{3}^2 + c_y t_{3} + d_y#
n_x2 = -(3a_y t_{3}^2 + 2b_y t_3 +c_y)#
n_y2 = 3a_x t_{3}^2 + 2b_x t_3 +c_x
} right none
}newline newline
alignl {
(x_1 - x)^2 + (y_1 - y)^2 = (a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - x)^2+(a_y t_{3}^3 + b_y t_{3}^2 + c_y t_3 + d_y - y)^2
} newline newline
alignl {
t_3 in [0;1]
}newline newline
alignl {
left lbrace alignl stack{
x_1+ n_x1 t_1 = a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - t_2(3a_y t_{3}^2 + 2b_y t_3 +c_y)#
y_1+t_1 n_y1 = a_y t_{3}^3 + b_y t_{3}^2 + c_y t_{3} + d_y + t_2 (3a_x t_{3}^2 + 2b_x t_3 +c_x)#
(x_1 - x_1+ n_x1 t_1)^2 + (y_1 - y_1+t_1 n_y1)^2 = (a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - x_1+ n_x1 t_1)^2+(a_y t_{3}^3 + b_y t_{3}^2 + c_y t_3 + d_y - y_1+t_1 n_y1)^2
} right none
}newline newline
alignl {
t_3 in [0;1]
}newline newline
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 13:28
Nick
Вот такие получились производные:

Код: Выделить всё
left lbrace alignl stack{
x = x_1+t_1 n_x1#y = y_1+t_1 n_y1
} right none
newline newline
left lbrace alignl stack{
x = x_2+t_2 n_x2#
y = y_2+t_2 n_y2#
x_2 = a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x#
y_2 = a_y t_{3}^3 + b_y t_{3}^2 + c_y t_{3} + d_y#
n_x2 = -(3a_y t_{3}^2 + 2b_y t_3 +c_y)#
n_y2 = 3a_x t_{3}^2 + 2b_x t_3 +c_x
} right none
newline newline
(x_1 - x)^2 + (y_1 - y)^2 = (a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - x)^2+(a_y t_{3}^3 + b_y t_{3}^2 + c_y t_3 + d_y - y)^2
newline newline
t_3 in [0;1]
newline newline
left lbrace alignl stack{
x_1+ n_x1 t_1 = a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - t_2(3a_y t_{3}^2 + 2b_y t_3 +c_y)#
y_1+t_1 n_y1 = a_y t_{3}^3 + b_y t_{3}^2 + c_y t_{3} + d_y + t_2 (3a_x t_{3}^2 + 2b_x t_3 +c_x)#
(x_1 - x_1- n_x1 t_1)^2 + (y_1 - y_1-t_1 n_y1)^2 = (a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - x_1- n_x1 t_1)^2+(a_y t_{3}^3 + b_y t_{3}^2 + c_y t_3 + d_y - y_1-t_1 n_y1)^2
} right none
newline newline
t_3 in [0;1]
newline newline
left lbrace alignl stack{
x_1+ n_x1 t_1 - (a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x) + t_2(3a_y t_{3}^2 + 2b_y t_3 +c_y) = 0#
y_1+ n_y1 t_1 - (a_y t_{3}^3 + b_y t_{3}^2 + c_y t_{3} + d_y) - t_2 (3a_x t_{3}^2 + 2b_x t_3 +c_x) = 0#
(n_x1 t_1)^2 + (n_y1 t_1)^2 - (a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - x_1- n_x1 t_1)^2 - (a_y t_{3}^3 + b_y t_{3}^2 + c_y t_3 + d_y - y_1 - t_1 n_y1)^2 = 0
} right none
newline newline
left [ matrix{
n_x1 #
3a_y t_{3}^2 + 2b_y t_3 +c_y #
-(3a_x t_{3}^2 + 2b_x t_3 +c_x) + t_2(6a_y t_3 + 2b_y) ##
n_y1 #
-(3a_x t_{3}^2 + 2b_x t_3 +c_x) #
-(3a_y t_{3}^2 + 2b_y t_3 +c_y) - t_2(6a_x t_3 + 2b_x) ##
2(n_x1^2+n_y1^2) t_1 + 2n_x1 (a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - x_1- n_x1 t_1) +2n_y1(a_y t_{3}^3 + b_y t_{3}^2 + c_y t_3 + d_y - y_1-t_1 n_y1) #0 #
-2(3a_x t_{3}^2 + 2b_x t_3 +c_x)(a_x t_{3}^3 + b_x t_{3}^2 + c_x t_{3} + d_x - x_1- n_x1 t_1) - 2(3a_y t_{3}^2 + 2b_y t_3 +c_y) (a_y t_{3}^3 + b_y t_{3}^2 + c_y t_3 + d_y - y_1-t_1 n_y1)
}right ]
newline newline
Введем обознаяения fx'(t3), fy'(t3), fx(t3), fy(t3)
newline newline
left [ matrix{
n_x1 #
fy'(t_3) #
-fx'(t_3) + t_2(6a_y t_3 + 2b_y) ##
n_y1 #
-fx'(t_3) #
-fy'(t_3) - t_2(6a_x t_3 + 2b_x) ##
2(n_x1^2+n_y1^2) t_1 + 2n_x1 (fx(t_3) - x_1- n_x1 t_1) +2n_y1(fy(t_3) - y_1-t_1 n_y1) #0 #
-2fx'(t_3)(fx(t_3) - x_1- n_x1 t_1) - 2fy'(t_3)(fy(t_3) - y_1-t_1 n_y1)
}right ]
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 16:17
Nick
Ура!!! Я кажется нашел точку G!!!



Искал как и описывал ранее.
При этом, что интересно, процедура получилась всего 50 строк!!!
PS Интересно, сколько народу сюда попадет по запросу "Я кажется нашел точку G" или "точка G"



PSS И сколько будет ее искать по методу Ньютона



Код: Выделить всё
def find_cutter_center((x1,y1),(nx1,ny1), sp1,sp2):
bez = (sp1[1][:],sp1[2][:],sp2[0][:],sp2[1][:])
ax,ay,bx,by,cx,cy,dx,dy=bezmisc.bezierparameterize(bez)
d,t3 = get_distance_from_point_to_csp((x1,y1),sp1,sp2)
t = numpy.matrix([[d/math.sqrt(nx1**2+ny1**2)],[1./2],[t3]])
fx,fy = bezmisc.bezierpointatt(bez,t3)
i = 0
ta = []
while i==0 or abs(F.sum())>straight_distance_tolerance and i<10:
ta += [t]
print_()
print_()
print_()
print_()
print_(t)
print_()
t1,t2,t3 = t.transpose().getA()[0]
fx,fy = bezmisc.bezierpointatt(bez,t3)
f1x,f1y = bezmisc.bezierslopeatt(bez,t3)
i+=1
F = numpy.matrix(
[
x1+nx1*t1-fx+t2*f1y,
y1+ny1*t1-fy-t2*f1x,
(nx1**2+ny1**2)*(t1**2) - (fx-x1-nx1*t1)**2 -(fy-y1-ny1*t1)**2
])
print_(F)
print_(F.sum())
F1 = numpy.matrix(
[
[
nx1, f1y, -f1x+t2*(6*ay*t3+2*by)
],
[
ny1, -f1x, -f1y-t2*(6*ax*t3+2*bx)
],
[
2*(nx1**2+ny1**2)*t1+2*nx1*(fx-x1-nx1*t1) +2*ny1*(fy-y1-ny1*t1),
0,
-2*f1x*(fx-x1-nx1*t1) -2*f1y*(fy-y1-ny1*t1)
]
]
)
print_()
print_(F1)
if numpy.linalg.det(F1) !=0:
print_()
print_(numpy.linalg.inv(F1))
t = t - numpy.linalg.inv(F1)*(F.transpose())
else: break
return t
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 17:07
dormouse
Как найти точку G? Подарок к 8 марта! Легко и просто! Не отнимет много времени! Попробуйте прямо сегодня!
Для движения по исходному OB (синему) контуру мы должны разбить кривую на минимальный шаг dl=длина_куска_кривой(Bi,B_{i+1}) была достаточно мала, чтоб ds=|B0,B1|=|B_i,B_{i+1}| (между точками) оказалась меньше погрешности "m". Вывод этого алгоритма думаю вовсе не отрисовывать кривыми безье - достаточно дуг или отрезков при малом шаге dl. Шириной или цветом каждого такого отрезка можно закодировать соответствующую глубину в результирующем G-коде.
P.S. Так же важно изначально помещать центр окружности G с некоторым сдвигом "m" в сторону "от кривой {B1,B2}", чтобы не было ложного самопересечения в точке Bi.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 17:38
Nick
dormouse писал(а):Для движения по исходному OB (синему) контуру мы должны разбить кривую на минимальный шаг dl=длина_куска_кривой(Bi,B_{i+1}) мала, чтоб ds=|B0,B1|=|B_i,B_{i+1}| (между точками) оказалась меньше погрешности "m". Вывод этого алгоритма думаю вовсе не отрисовывать кривыми безье - достаточно дуг или отрезков при малом шаге dl. Шириной или цветом каждого такого отрезка можно закодировать соответствующую глубину в результирующем G-коде.
Имхо можно сделать так: делим отрезок (B_i,B_{i+1}) на несколько частей, делаем для них отступ и по получившимся точкам строим новую кривую.
dormouse писал(а):P.S. Так же важно изначально помещать центр окружности G с некоторым сдвигом "m" в сторону "от кривой {B1,B2}", чтобы не было ложного самопересечения в точке Bi.
Не совсем понял, какое ложное пересечение?
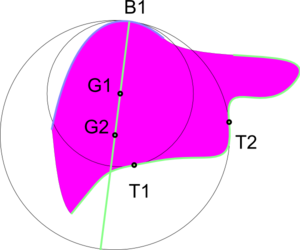
ЗЫ вот такая картинка получилась (можно сравнить с нарисованной вручную)
Одна окружность попала мимо, т.к. нет проверки пересечения с ближним краем, только с противоположной стороной угла.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 17:46
dormouse
Возможно, на это я и указывал -- ложные срабатывания в точках Bi. А так - сама кривая (у неё может быть в районе точки B_{i+1} БУГОРОК до точки G =) ), поэтому ВСЕ кривые должны быть в цикле на проверку. Для исключения точки B_i я предложил бы сместить точку G немного вверх по нормали в сторону "от" исходного контура (точки B_i).
Путём поиска нашёл решённое до нас:
www.algorithmist.net/closestcubic.html и сам код wired.freehep.org/xref/hep/wired/heprep/util/NearestPoint.html и теорию pvnick.blogspot.com/2010/01/im-currently-working-on-project-that.html
Так же стало понятно что такое длина кривой безье =)
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 18:07
Nick
Не особо вчитываясь в код, я понял, что они не решают уравнение пятой степени, а просто делят безье его на кучу частей и аппроксимируют ломанной. Я правильно понял?
У меня функция нахождения ближней точки на безье получилась проще 11 строк:
Просто выбираем n точек на безье, считаем минимальное расстояние до них. Затем выбираем 2*n точек и сравниваем разницу вычислений. Если она меньше погрешности, то возвращаем результат.
Код: Выделить всё
def get_distance_from_point_to_csp(p,sp1,sp2, tolerance = 0.01 ):
n, i = 10, 0
d, dl = [None,(0,0)],[0,(0,0)]
while i<2 or (abs(d[0]-dl[0])>tolerance and i<4):
i += 1
dl = d[:]
for j in range(n+1):
t = float(j)/n
cp = csp_at_t(sp1,sp2,t)
d = min( [(P(cp)-P(p)).mag(),t], d) if d[0]!=None else [(P(cp)-P(p)).mag(),t]
n=n*2
return d
Кстати это не наша задача, т.к. мы не знали заранее точку от которой нужно искать расстояние. Не знали где точка G

.
Мне сейчас нужно найти построение кривой безье проходящей через точки.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 18:19
dormouse
Нам надо было искать максимальное решение:
Найти координаты точки G для каждой точки B на замкнутой кривой C, лежащей на нормали (внутри С), такую что |BG| максимально и |GBi|<|GB| для любой точки Bi и |GB|<R.
Для точки B=Bi надо сделать исключение =)
P.S. Я думаю что если строить кривую безье по полученным G-точкам, то это будет намного более продвинутый метод нежели имеющийся сейчас для Area curves!
Для генерации G-кода более уместна ломаная с переменной шириной=Глубине.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 18:28
Nick
dormouse писал(а):Я думаю что если строить кривую безье по полученным G-точкам, то это будет намного более продвинутый метод нежели имеющийся сейчас для Area curves!Для генерации G-кода более уместна ломаная с переменной шириной=Глубине.
Новая кривая безье - это траектория инструмента, ее сразу можно переводить в Gкод имеющейся функцией.
Построить ее проще чем делать полноценный отступ, с отступом все сложнее там нужно делать клиппинг, а это жесть!
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 03 мар 2010, 19:37
dormouse
Если закладываться только на V- и U- образные "носики" для конической фрезы, то имеет смысл ограничиваться разноширинной ломаной и результирующая кривая безье вовсе не нужна.
Если это для полноценной замены Inkscape'овского оффсета, то надо строить. Так же важно не забывать, что любая подобная операция может разбивать исходный контур на несколько несвязанных областей, что "условно" незаметно для нулевого радиуса конической фрезы, т.к. бесконечно близкие части исходной синей кривой не очень вероятны.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 04 мар 2010, 14:52
dormouse
Определение (траектория для конической фрезы):
Это ГМТ (геометрическое место всех точек) G таких, что ∀ (для любой) т. B ∈ (принадлежащей) исходной кривой C и нормали (направленной внуть контура) из т.B выполняются условия |BG|≤Rmax и ω(G,|BG|)∩C={B}
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 04 мар 2010, 23:56
Nick
dormouse писал(а):Определение (траектория для конической фрезы):
Это ГМТ (геометрическое место всех точек) G таких, что ∀ (для любой) т. B ∈ (принадлежащей) исходной кривой C и нормали (направленной внуть контура) из т.B выполняются условия |BG|≤Rmax и ω(G,|BG|)∩C={B}
Это в идеальном случае, а у нас чуть по-другому:
|BG|≤Rmax заменить на abs(|BG|-Rmax)<eps (eps - эпсилон - погрешность) с пересечением тоже не совсем ясно (могут быть точки на другой стороне, которых фреза касается).
By the way, Ура! Я, несмотря на все убеждения

, вычислил безье. Причем это получилось в 6 строк

Код: Выделить всё
m += [ [ti**3,3*(1-ti)*(ti**2),3*((1-ti)**2)*ti, (1-ti)**3] ]
xi += [ [x1+nx*r,y1+ny*r] ]
m = numpy.array(m)
xi = numpy.array(xi)
sp1,sp2 = [[0.,0.],[0.,0.],[0.,0.]], [[0.,0.],[0.,0.],[0.,0.]]
a,b,c,d = numpy.linalg.solve(m, xi).tolist()
Есть только одна проблема, не совсем понятно как рассчитывать расстояние до отрезков этого же (не противоположного) края угла. С перпендикулярами все понятно, но при проверки расстояний до точек противоположного края, расстояние до перпендикуляра |BG| сравнивается с половинным расстоянием до крайних точек сегментов |BT_j|/2 и |BT_{j+1}|/2. с ближним краем это не пройдет, т.к. тогда D< min|B B_j| ∀j=1..n.
Добавил сравнение с диаметром инструмента:
Версия пока не рабочая!
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 05 мар 2010, 10:49
Nick
root писал(а):Есть только одна проблема, не совсем понятно как рассчитывать расстояние до отрезков этого же (не противоположного) края угла. С перпендикулярами все понятно, но при проверки расстояний до точек противоположного края, расстояние до перпендикуляра |BG| сравнивается с половинным расстоянием до крайних точек сегментов |BT_j|/2 и |BT_{j+1}|/2. с ближним краем это не пройдет, т.к. тогда D< min|B B_j| ∀j=1..n.
Придумал как решить эту проблему:
Сравнение нужно проводить не с половиной расстояния до точки другого отрезка кривой |BT_j|/2 и |BT_{j+1}|/2, а вместо этого вычислять такую же вписанную окружность как и для не граничных точек участка кривой, только с более простыми условиями:
1. Мы знаем, что центр окружности лежит на нормали.
2. Мы знаем точки касания (T_i и B_i).
Т.е. решаем систему:
Код: Выделить всё
left lbrace alignl stack{
x = B_ix+t_1 n_x1#y = B_iy+t_1 n_y1#
(x-B_ix)^2 + (y-B_iy)^2 = (x-T_ix)^2 + (y-T_iy)^2
} right none
newline newline
Пусть, (x_1,y_1)=(B_ix,B_iy), (x_2,y_2)=(T_ix,T_iy)newline newline
left lbrace alignl stack{
x = x_1+t_1 n_x1#y = y_1+t_1 n_y1#
(x-x_1)^2 + (y-y_1)^2 = (x-x_2)^2 + (y-y_2)^2
} right none
newline newline
left lbrace alignl stack{
x = x_1+t_1 n_x1#y = y_1+t_1 n_y1#
(x_1+t_1 n_x1-x_1)^2 + (y_1+t_1 n_y1-y_1)^2 = (x_1+t_1 n_x1-x_2)^2 + (y_1+t_1 n_y1-y_2)^2
} right none
newline newline
left lbrace alignl stack{
x = x_1+t_1 n_x1#y = y_1+t_1 n_y1#
n_x1^2 t_1^2 +n_y1^2 t_1^2 = n_x1^2 t_1^2 +x_1^2+x_2^2+2x_1 n_x1 t_1 -2x_2 n_x1 t_1 -2x_2 x_1 +n_y1^2 t_1^2 +y_1^2 + y_2^2 + 2y_1 n_y1 t_1 -2 y_2 n_y1 t_1 -2y_1 y_2
} right none
newline newline
left lbrace alignl stack{
x = x_1+t_1 n_x1#y = y_1+t_1 n_y1#
(2x_1 n_x1- 2x_2 n_x1 + 2y_1 n_y1 -2 y_2 n_y1)t_1 = 2x_1 x_2 + 2y_1 y_2 - x_1^2 -x_2^2 -y_1^2 - y_2^2
} right none
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 05 мар 2010, 13:08
dormouse
Никак не могу понять суть проблемы. Требуется иллюстрация.
Алгоритм планируется сделать двухпроходным как с AreaCurves? В чём вообще смысл отрисовывания средней линии? Для построения G-кода по ней необходимо будет заново рассчитывать расстояния до БЛИЖНЕЙ точки всего контура C в каждой точке этой кривой! Фактически, эта операция уже раз проводится на стадии вычисления опорных точек средней линии...
Тупо скачал последний вариант ("не рабочий из прошлого поста").
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 05 мар 2010, 14:39
Nick
dormouse писал(а):Алгоритм планируется сделать двухпроходным как с AreaCurves? В чём вообще смысл отрисовывания средней линии? Для построения G-кода по ней необходимо будет заново рассчитывать расстояния до БЛИЖНЕЙ точки всего контура C в каждой точке этой кривой! Фактически, эта операция уже раз проводится на стадии вычисления опорных точек средней линии...
Нет, не придется. Для экспорта в Gкод используется процедура biarc, в которую передается сегмент кривой, и глубина в начале и в конце сегмента, т.е. построив кривую траектории мы можем натравить на нее процедуру biarc и получить Gкод.
dormouse писал(а):Тупо скачал последний вариант ("не рабочий из прошлого поста").
Ну я же написал "не рабочий"

.
Просто иногда я пользуюсь форумом как файлообменником, чтобы перетащить программу с работы домой и обратно

.
А! Понял откуда у тебя ошибка! Нужно было смотреть в самом верху:
"Directory does not exist!"
Директория, которую ты указал не существует!
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 05 мар 2010, 14:57
dormouse
как мы узнаем глубины "потом", на втором проходе? Или я сильно отвлёкся и не могу ухватить суть беседы?
1. AreaCurves "условно-ненужный", т.к. это просто дубликат--динамическая втяжка--G-code, но с клавиатуры вводятся числа отступа. ( при обычном ручном методе я так и не увидел глюков, т.е. при уширяем контур в режиме "округлости" и преобразование его в путь).
2. Алгоритм средней линии заменить нечем из стандартного арсенала. После его работы остаётся кривая со значением радиуса (ширины) в каждой точке. Мне казалось, что сохранить внутри узлов эту информацию представляется возможным только цветом либо шириной контура (самый наглядный путь) -- можно сделать разрывные безье-фрагменты чтоб разная ширина хранилась.
Поясните, пожалуйста, каким образом мы будем узнавать глубину на стадии формирования G-кода?
P.S. Ошибка, приведённая ранее показывается и на других версиях скрипта. Лечится убиранием self.header/footer из кода. я так и не понял, почему инициализация не проходит.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 05 мар 2010, 17:40
Nick
dormouse писал(а):как мы узнаем глубины "потом", на втором проходе? Или я сильно отвлёкся и не могу ухватить суть беседы?
1. AreaCurves "условно-ненужный", т.к. это просто дубликат--динамическая втяжка--G-code, но с клавиатуры вводятся числа отступа. ( при обычном ручном методе я так и не увидел глюков, т.е. при уширяем контур в режиме "округлости" и преобразование его в путь).
2. Алгоритм средней линии заменить нечем из стандартного арсенала. После его работы остаётся кривая со значением радиуса (ширины) в каждой точке. Мне казалось, что сохранить внутри узлов эту информацию представляется возможным только цветом либо шириной контура (самый наглядный путь) -- можно сделать разрывные безье-фрагменты чтоб разная ширина хранилась.
Поясните, пожалуйста, каким образом мы будем узнавать глубину на стадии формирования G-кода?
1. В процессе вычисления кривой находятся необходимые заглубления.
2. Если мы хотим сразу все конвертировать в Gкод, то, по большому счету, можно даже эту кривую не рисовать, сразу вычисляем Gкод для всех сегментов кривой. (Функция для вычисления Gкода уже есть - это часть Path to Gcode). Как я уже писал, зная сегмент кривой, заглубление в начале сегмента и в конце сегмента пишем biarc(sp1,sp2, z1,z2) (для аппроксимации сегмента биарками) потом generate_gcode (функция организует вывод внутреннего формата в Gкод) и получаем необходимый Gcode
3. Конечно можно нарисовать кривую, с переменной толщиной штриха и дать пользователю возможность ее отредактировать перед экспортом...
P.S. Ошибка, приведённая ранее показывается и на других версиях скрипта. Лечится убиранием self.header/footer из кода. я так и не понял, почему инициализация не проходит.
Не проходит потому, что это небольшой баг. Я вынес процедуру проверки наличия директория в отдельную функцию. Она проверяет, если директория не существует, то выдать ошибку + "return" раньше это означало, выход из программы, а теперь только выдает ошибку "Directory does not exists" и идет дальше но при этом не назначает header и footer, что вызывает последующие ошибки. Исправил в новой версии, но она пока не готова и ее использовать не надо!
Единственное, что меня может оправдать, что в любом случае вывода Gкода быть не должно, т.к. некуда выводить - директория нет!
Столкнулся с проблемой:
1. Я убрал правую и левую части контура.
2. Теперь для вычисления отступа пробегаемся по всем сегментам.
Но появляется проблема с углом:
Если при вычислении отступа учитывать соседние элементы, то на конце отрезка минимальная ближайшая точка - начало следующего отрезка, т.е. 0 (нижняя часть рисунка), а если не учитывать соседние сегменты, то получается что в угле образуется проблема (верхняя часть рисунка).
Чтобы такое придумать

?
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 05 мар 2010, 19:34
Nick
Размышления на тему как определить угол.
Ну тут в принципе также как и в оффсете измеряем угол между касательными/нормалями в точке соприкосновения и далее если угол не равен нулю, то вычисляем следующие параметры:
если вершина угла, первая касательная и вторая касательная образуют правую тройку точек и угол острый, то угол внутренний и нужно его вырезать, т.е. сводить заглубление к 0 и приближаться к углу. Если наоборот, то угол внешний и нужно нарисовать окружность из одной предыдущей точки до следующей с постоянным заглублением.
Если угол между касательными равен 0 то угла нет и точку соприкосновения не берем.
Второй вопрос как проверит нет ли пересечений с тем же самым сегментом? Та система которую мы регали по идее может дать несколько решений, и их нужно отделить перед тем как применять к ним метод Ньютона. Можно просто взять 12 точек t=0.0, 0.1, , ..., 0.9, 1 и применить к ним метод Ньютона. Выбрать миимальный не нулевой корень.