Страница 4 из 39
Разработка Gcodetools - плагин Inkscape для экспорта в Gкод
Добавлено: 07 дек 2009, 11:39
Nick
Разработка Gcodetools
Эта ветка посвящена разработке
Gcodetools, плагина для векторного редактора
Inkscape, позволяющего конвертировать кривые из Inkscape в Gкод, используя круговую и линейную интерполяцию.
Описание работы, установка, помошь и уроки по плагину можно найти в теме:
Gcodetools - plug-in Inkscape для экспорта в Gcode
На данный момент ведется работа над Gcodetools 1.7
Что мы хотим увидеть в новой версии:
- Улучшение расширения для плазменной резки
- Добавление дополнительных опций экспорта:
- Улучшение функции обработки площади
- Угол заглубления
- Расширение для сверловки
Требуются
- Тестеры
- Разработчики
- Помощь в технических аспектах по работе станков и обработке материалов
- Новые идеи
Последняя версия
Исходный код находится на launchpad.net. Получить последнюю версию при помощи bazaar можно так:
Последнюю версию можно загрузить через web-интерфейс:
http://bazaar.launchpad.net/~gcodetools ... lope/files
Установка
1. Загрузите последнюю ревизию, из указанных выше мест.
2. Выполните "python create_inx.py" в директории с загруженными файлами.
3. Скопируйте все созданные файлы с расширением *.inx и файл gcodetools-dev.py в каталог:
Linux: /usr/share/inkscape/extensions/ и перезапустите inkscape
Windows: Program Files\Inkscape\share\extensions\
4. Перезапустите Inkscape
Последняя версия может быть не рабочей! Для получения стабильной рабочей версии зайдите сюда
Gcodetools - plug-in Inkscape для экспорта в Gcode или загрузите предыдущие ревизии.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 27 фев 2010, 19:26
dormouse
>Карту высот можно задать битмапом. Т.е. просто вставить битмап в инкскейп и все.
Для этого кто-то где-то как-то должен перед этим его нарисовать. Хочется "унификации".
>Я вот тут подумал, а не логичнее ли будет делать такой уголок шариком? Тогда и борозды посередине не >останется и края будут плавно закругляться...
Оптимально на 3 фрезы раскладывать: a)4..10мм цилиндр, b)3..4мм шарик (можно небольшой гарельеф сделать) или цилинд с шаровым окончанием(Dшара=Dцилиндра, можно дорезать контур где надо), c)2..5мм конус
Так получается, что a) проходит всю чернуху и утопленные плашки, b) все "синие озерца", плавные "U"-стыки исходного контура и серые карты глубин (если такие вставки нужны) c) все "V"-стыки (без радиуса скругления) + фаски + мелкие детали
Уйти от этой технологии мне видится невозможным, т.к. : a) не даст никакой картинки с достаточным качеством, b) универсальная, но долго надо работать ( чтоб контура внизу шарика сошлись надо выставить шаг ~0.3мм), c) вообще плоскости невозможно выбрать
Можно сразу полноценную 3-х фрезную версию делать. Это самый адекватный и нужный подход =)
P.S. Обратите внимание! Я отредактировал предыдущее сообщение -- там сбивающая с толку картинка приведена была. Она просто некорректная. Добавлен рис 5а.
P.P.S. Полагаю, можно сделать картинку на Python скрипте и "обновлять её содержимое" ? Если да, то напишем очень важную вещь - сразу же и встроенный Preview/back-plotter/g-code emulator, т.е. что именно вырежется из сгенерированного g-code этими фрезами.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 27 фев 2010, 23:54
Nick
А чем плох такой вариант:
Сначала проходим контур с оффсетом -2D цилиндром:
Потом уточняем границу конусом:
Потом рисуем угол - конусом по центру угла постепенно поднимаясь:
На картинке видна грань при обработке угла, но ее быть не должно (это дефект рендера)
Нужно: Диаметр конуса >=d, глубина >= d*tg(угла наклона конуса).
Плюсы: не будет дефектов, плавные переходы граней.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 28 фев 2010, 00:04
dormouse
Основная проблема в том, что НЕ ВСЕГДА(!) нужна фаска на основной рабочей длине контура детали!! Если возможно - надо перейти в ICQ/skype. Читайте Л.С.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 28 фев 2010, 21:16
Nick
У нас есть две задачи: найти те места где не прошел цилиндр, вычислить траекторию для этих мест.
В общем случае задачи не тривиальны. Для поиска узких мест нужно вычислять расстояния от каждой точки кривой до каждой точки кривой. Аналитически такая задача не решается методы вычей будут требовать большого времени. По идее для вычисления минимального расстояния с приличной точностью придется 10-100 промежуточных точек каждого сегмента итого сложность получится n^2*m^2 где n количество сегментов, а m количество промежуточных точек. Как-то много.

Построение траектории по проще. Предположим мы нашли угол, знаем его вершину. Тогда нам нужно построить две кривых между правой и левой частью угла. Каждая кривая должна выходить из вершины угла и расстояние от кривой до стороны угла в каждой точке должно быть равно половине диаметра фрезы если толщина контура в этой точке больше диаметра фрезы и половине толщины контура в этой точке, если она меньше диаметра фрезы.
Для случая ломанной нужно просто разбить обе стороны угла таким образом, чтобы длины сегментов у правой и левой сторон были одинаковыми и интерполировать контрольные точки.
Для кривых безье все сложнее, не уверен, что такую кривую можно описать кривой безье того же класса как и стороны угла. Но можно строить приближения таким же образом как с ломанной и если надо уменьшать длину сегментов.
PS в icq так и не смог до тебя вчера достучаться.
Pss писал с телефона, прошу прощения за очепятки

.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 01 мар 2010, 11:47
Nick
Подправил один баг и вот что на данный момент получилось

:
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 01 мар 2010, 16:12
Nick
Пока никак не получается сделать нормальный оффсет с переменным радиусом

.
Предположим мы хотим найти отступ в точке А. Т.е. нам нужно найти точку О.
Ясно, что она лежит на перпендикуляре к кривой.
Как найти расстояние от А до О??? 
Я нарисовал несколько возможных случаев.
Красная линия - перпендикуляр в точке А
Точка B - точка на противоположной стороне контура, которая учитывается при поиске радиуса.
Зеленая линия - ближайшая точка на противоположном контуре.
Синяя нормаль в точке В.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 01 мар 2010, 18:26
dormouse
Bugs:
1. (inkscape 0.47-3/windows) после работы Area curves нельзя выделить контур (только наводишь мышку, становится красным, потом сразу обратно чёрным) - лечится "экспорт в .ps" и импорт обратно.
2. плагин вообще не работает из-за жёстко прописанного пути к логам - надо как-то исправить путь "/home/nick/", ручная правка спасает положение =)
3. очень много артефактов (в посторонних местах непонятные штрихи) при отступе Area distance больше 1/2 ширины вырезаемых карманов
Написал мысли в сегодняшнем числе (красная надпись 20100301), раздел Inkscape.
http://www.kalyaev.com/2010/pub.html
Отдельно привожу фото.
* Синий цвет - оригинальный контур исходного файла
* Серая заливка - желаемая деталь.
* Чёрный цвет - траектория цилиндра 1
* зеленоватый - реальная выборка им
* сиреневый - траектория малой скруглённой фрезы 2
* красный - траектория треугольной фрезы 3
Нас интересуют "треугольники" AOB. Путь GO от красной конической фрезы 3. В точке G заглубление максимально (визуально красная линия повторяет контур BO примерно от точки D). Отступ |BO,G|=d конической фрезы 3. На отрезке DO заглубление спадает до нуля (в т. O).
Сиреневая траектория CD - примерный путь цилиндрической фрезы 2 с шариком на конце (скруглённой).
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 01 мар 2010, 18:57
Nick
dormouse писал(а):Bugs:
1. (inkscape 0.47-3/windows) после работы Area curves нельзя выделить контур (только наводишь мышку, становится красным, потом сразу обратно чёрным) - лечится "экспорт в .ps" и импорт обратно.
2. плагин вообще не работает из-за жёстко прописанного пути к логам - надо как-то исправить путь "/home/nick/", ручная правка спасает положение =)
3. очень много артефактов (в посторонних местах непонятные штрихи) при отступе Area distance больше 1/2 ширины вырезаемых карманов
1. Какая версия? Из шапки или нет? Как вариант, перед применением Area curves выделить контур + Контур -> Динамическая втяжка (Ctrl + J). Inkscape перед задачей offset каким-то образом преобразует контур, я попытался это повторить, но не всегда работает как надо

.
2. Упс... Закомментировал функцию логов. Исправил шапку.
3. Функция вычисления кривых площади использует инкскейповский dynamic offset. Он дает артефакты. Вобще, задача оффсета далеко не тривиальная и обычно требует очень большого количества вычислений. Я честно пытался написать собственный оффсет, но из этого мало что получилось. Точнее получилось, но он все равно глючил и работал очень медленно. Самое сложное сделать клиппинг, для него считается оффсет в две стороны (внутрь и наружу) и рассчитываются их взаимопересечения. Сложность O(n^2) при размере контура 500 контрольных узлов дождаться конца обработки практически нереально.

dormouse писал(а):Bugs:
Нас интересуют "треугольники" AOB. Путь GO от красной конической фрезы 3. В точке G заглубление максимально (визуально красная линия повторяет контур BO примерно от точки D). Отступ |BO,G|=d конической фрезы 3. На отрезке DO заглубление спадает до нуля (в т. O).
Главный вопрос, как рассчитать положение точки D? Как рассчитать расстояние от контура до траектории за точкой D, т.е. ближе к углу?
Как быть в таких случаях:
Как найти угол?
По идее нужно обрабатывать не две стороны, а просто идти по контуру с отступом. Но как этот отступ рассчитать?
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 01 мар 2010, 23:52
dormouse
1. Всё было последним. Ctrl+j (динамическую втяжку) попробовал. Сам путь после этого вроде перестал по узлам выделяться, но результат стал похож на желаемый. Надо побольше времени на тестирование.
2. Логи не надо выключать. Надо добавить поле "путь для лог файла" в .inx интерфейс!!
3. Вместо Dynamic offset -- посмотрите мой путь: утолщаем контур (ширина линии, в растровом варианте -- вокруг каждого
пиксела границы нарисовать круг диаметром нужной ширины линии),
преобразуем в путь, break apart, удаляем внешний контур. Получаем ЖЕЛАЕМЫЙ(!)
результат (проверяется утолщением на ту же величину в режиме "скругления"
на изломах)
----
Решение I: простое и очевидное -- идти от точки B в сторону точки O и далее до точки A по правилу максимальный отступ от желаемой синей линии вплоть до ½d, но не касаясь ни одной синей линии. При этом отступ по нормали от синей линии равен ширине фрезерования и по формуле равен глубине (предполагаем, что ширина=функция(глубины), взаимнооднозначная, в простейшем случае ширина=глубина для 45° конуса).
Решение II. Нарисовать ГРАДИЕНТНОЕ уширение линии (градиент(l)=функция(глубины фрезы на этом диаметре)) вместо обычного (чёрный цвет-линия, белый при l>½d, фактически это получится Z-depth map дл). После этого все места, где синие контура ближе чем ½d друг к другу будут нарисованы как не-белые куски, отстоящие от белых лужиц в середине.
Решение III.
1. заливаем снаружи от синего контура 50% серым.
2. делаем границу салатового скруглённого контура (от фрезы 1) зелёным.
3. вычитаем из синего контура зелёный и закрываем полученные синие U- и V- образные "оглобли" (для более сложного варианта замыкать можно другим цветом, если Inkscape это поддерживает)
4. полученные замкнутые кривые (синяя граница, серое содержимое) обрабатываем отдельно -- как без скрипта сделать (пока) не придумал.
Для генерации G-code таким образом имеем карту глубин, которую переводим в простейший набор линий.
P.S. В самом крайнем случае если нарисовать градиент, то уже готова обычная Z-depth map для конической фрезы (учитывая небольшой % от общей площади это может быть достойным решением.... но, конечно одну "правильную" линию это с художественной точки зрения не заменит).
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 11:46
Nick
dormouse писал(а):1. Всё было последним. Ctrl+j (динамическую втяжку) попробовал. Сам путь после этого вроде перестал по узлам выделяться, но результат стал похож на желаемый. Надо побольше времени на тестирование.
2. Логи не надо выключать. Надо добавить поле "путь для лог файла" в .inx интерфейс!!
3. Вместо Dynamic offset -- посмотрите мой путь: утолщаем контур (ширина линии, в растровом варианте -- вокруг каждого
пиксела границы нарисовать круг диаметром нужной ширины линии),
преобразуем в путь, break apart, удаляем внешний контур. Получаем ЖЕЛАЕМЫЙ(!)
результат (проверяется утолщением на ту же величину в режиме "скругления"
на изломах)
1. По узлам не выделяется потому, что это теперь dynamic offset а не path. У него только одна контрольная точка которая отвечает за радиус оффсета. Кстати похоже в прошлый раз у тебя была такая же проблема, если выделять такой объект припомощи F2, то он при наведении становится синий, а при выделении становится черный, при этом вокруг него появляется обводка и одна контрольная точка. Т.к. объект у тебя составной, то обводки при увеличении ты мог не увидеть.
Почему при экспорте в эпс все работало нормально работать:
Внутренняя структура svg такова: если объект контур у него есть параметр "d" в нем описывается геометрия контура. Когда инкскейп создает оффсет, объект преобразуется, у него появляются поля: "sodipodi:offset" - говорит, что объект это оффсет, "inkscape:original" - содержит параметр "d" контура исходника, "inkscape:radius" - радиус оффсета, при этом для совместимости с обычным svg добавляется поле "d" в котором описывается результат оффсета. Когда ты сохранил в эпс inkscape просто перевел все оффсеты в path. Этого же можно добиться путем Контур - Оконтурить объект (Ctrl+Shift+C).
2. Это не совсем логи, это функция для отладки программы. Просто обычный print не подхоит, т.к. он пишет в стандартный поток из которого inkscape берет преобразованный svg, и если туда писать что-либо inkscape с большой вероятностью вылетит.
3. Эффект будет тот же. Я думаю, процедура оффсета и отрисовки контура одна и та же. См аттач.
По поводу решений: я все бьюсь над проблемой как вычислить положение точки центра фрезы.
Предположим мы идем от точки В к точке О. Для точки В1 нужно найти точку F1. Она лежит на нормали к кривой в точке В1, но
как рассчитать расстояние от В1 до F1? Меня интересует геометрическое решение, для которого можно написать алгоритм построения.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 12:47
dormouse
Я не очень понял смысл вопроса про поиск точки. Фактически требуется найти траекторию G5,G4,G3,G2,G1,G0 или 0 (зависит от того, есть ли минимальный диаметр у конуса, или он "бесконечно острый").
Работающий (идейно) метод: начинаем в точке B5 (это касание исходной фрезой 1 желаемого синего контура). Начинаем обходить контур от т. B5 в сторону O (всё время касаясь окружностью траектории кривой {B5,O}). В какой-то момент в точке (G4) происходит касание другого синего контура => начинаем уменьшать диаметр и приближать точку G3 к B3 (отрезок |B4G3| это шаг алгоритма, если растровый/сеточный метод) до тех пор, пока касание T3 не пропадёт (или не станет точечным, а не двух+ точечным). и т.п. вплоть до т. G0 или 0 (если контур V-образный конец, для U-образного остановка(поворот) произойдёт в фокусе закругления, если оно меньше диаметра конуса d3(max).
Написано не очень внятно, но для растровый алгоритм готов.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 13:23
123th
мой взгляд на построение.
1) в программе задаём количество фрез и их диаметры. т.е. нужна кнопка "добавить фрезу" которая будет добавлять фрезу с указанием типа и параметров для типа.
фрезы задаются по порядку прохождения. т.е. сначала самая большая, потом доводочные в порядке их смены (например сначала меньший цилиндр а потом конус, но не наоборот).
2) исходя из заданного набора фрез, программа строит пути:
2.1) сначала для первой фрезы. потом построенный путь обходится контуром равным диаметру первой фрезы.
2.2) далее начальный контур проходится диаметром инструмента 2 (строится путь для меньшей фрезы).
2.3) ищутся точки пересечения второго пути с результатом обхода пути 1 диаметром инструмента 1, вся часть пути 2 оказавшаяся внутри контура обхода диаметром 1 пути 1 удаляется.
3) повторять алгоритм для остальных инструментов если они есть.
****
для построения пути подъёма конусной фрезы в концах углов и в узких "перешейках":
пока что алгоритм для "не извивающихся" углов, т.е. имеющих средний путь в виде одной прямой или одной дуги.
для прямых линий всё просто: строим среднюю линию (начало в углу пути предыдущего пути обхода) и вычисляем перепады высот в точках излома, после чего можно скорректировать карту высоты для пути учитывая любые 2 из следующих параметров конусной фрезы: угол, высоту, макс. диаметр. (если конус не усечённый).
для углов образованных прямой и дугой, или двумя дугами:
строим окружность в любом месте между двумя линиями образующими угол, далее по трём точкам (вершина угла, центр окружности и угол предыдущего пути) строим кривую. это будет путь, как минимум очень близкий к нужному. карту высот строим градиентом, т.е. с указанным пользователем шагом считаем диаметр окружности вписанной между двумя стенками контура с центром на средней линии в точке шага.
если подумать то и построение пути для сложно изогнутых перешейков и концов контура осуществляется аналогично.
на картинке:
синий: начальный контур.
толстый зелёный: пути инструментов.
красный штрих-пунктир: контур того что получится при проходе инструмента 1 по пути 1.
синий штрих: путь инструмента для выборки угла.

Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 16:29
Nick
dormouse писал(а):В какой-то момент в точке (G4) происходит касание другого синего контура.
Как найти точку G4?
Смотрите что у нас заданно:
Две части угла - параметрическими кривыми, точка B1. Диаметр фрезы.
Можем вычислить нормаль в точке В1.
Если бы можно было построить точку G геометрически (при помощи циркуля и линейки) все было бы просто.
В противном случае имеем:
Две части кривой ОТ и ОВ, каждая задана несколькими сегментами.
Сегмент задается параметрически следующей формулой:
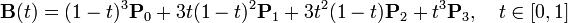
- 345cb15e836677e949b72ace996ac052.png (1.69 КБ) 7222 просмотра
- 300px-Bezier_curve.svg.png (4.2 КБ) 7222 просмотра
Пусть мы находимся в точке B1.
1. Мы знаем, что точка G1 лежит на нормали к кривой ВО в точке В1.
2. Мы знаем, что точка G1 лежит на нормали к кривой ТО, но не знаем где находится точка Т1
3. Мы не знаем расстояние от точки B1 до G1.
Для вычисления точки G1 нужно составить систему и решить ее.
Итак, первые два уравнения задают нормаль к ВО в точке В1:
x = x1+t1*dx
y = y1+t1*dy
dx,dy это значения производных в точке В1, их знаем
Еще два уравнения задают нормаль в производной точке TO
x = x2+t2*dx2
y = y2+t2*dy2
dx2 = 3*ax* t3^2 + 2*bx*t3 +cx
dy2 = 3*ay* t3^2 + 2*by*t3 +cy
ax,bx,cx,ay,by,cy - параметры задающие кривую, их знаем
и еще одно уравнение, задает равное расстояние |G1B1| и |G2B2|:
(B1.x - x)**2 + (B1.y - y)**2 = (ax*t3**3 + bx*t3**2 + cx*t3 + ex - x)**2 + (ay*t3**3 + by*t3**2 + cy*t3 + ey - y)**2
ax,bx,cx,ex,ay,by,cy,ey - параметры задающие кривую, их знаем.
Если решить эту систему относительно t1,t2,t3 найдем точку G1.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 16:48
Nick
Все это счастье дает систему из трех нелинейных уравнений. Причем последнее аж 6-ой степени

.
И как это решать?
x1+t1*dx = x2+t2*(3*ax* t3^2 + 2*bx*t3 +cx)
y1+t1*dy = y2+t2*(3*ay* t3^2 + 2*by*t3 +cy)
(B1.x - x1+t1*dx)**2 + (B1.y - x1+t1*dx)**2 = (ax*t3**3 + bx*t3**2 + cx*t3 + ex - x)**2 + (ay*t3**3 + by*t3**2 + cy*t3 + ey - y)**2
Хотя, численными методами решить можно... Нужно только найти начальное приближение...
Да и решать такую систему нужно для каждого сегмента кривой ОТ, и потом выбрать решение с минимальным G1.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 17:22
dormouse
Надо будет немного освежить параметрические задания кривой. Формулы лучше через OpenOffice или OpenOffice/latex вставлять - так сложновато понимать их, а только картинка не позволяет легко редактировать =).
Для примера через синтаксис OpenOffice Math:
рис 1. left lbrace alignl stack{x = x_1+t_1 dx#y = y_1+t_1 dy} right none
рис 2. left lbrace alignl stack{x = x_2+t_2 dx_2#y = y_2+t_2 dy_2#dx_2 = 3axt_{3}^2 + 2bxt_3 +cx#dy_2 = 3ayt_{3}^2 + 2byt_3 +cy} right none
рис 3. (B_1x - x)^2 + (B_1y - y)^2 = (axt_{3}^3 + bxt_{3}^2 + cxt_{3} + ex - x)^2+{}newline{}+(ayt_{3}^3 + byt_{3}^2 + cyt_3 + ey - y)^2
Синтаксис других программ лучше не использовать, т.к. преимущественно они все платные, либо "фиг установишь с квалификацией пользователя" =)
Учитывая третью степень, если решение легко не выйдет, то можно итеративно до появления корней наращивать координаты точек G *rofl*. Собственно предлагается вместо поиска корней (если будет сложно) подставлять константы конкретного фрагмента и конкретной окружности и искать пересечение. Для ускорения можно BBOX'ы для начала проверить - может они разнесены в пространстве...
Что-то мне кажется странным - это решение системы надо прогнать для всех сегментов исходной "синей" кривой, т.е. фрагментами между каждыми точками из режима редактирования? Мне надо теорию линий почитать. Я забыл - во всех ли точках можно такую кривую разбить на отдельные сегменты, или они как-то связаны математически (вроде влияния "через один узел" на форму кривой)
------------
Алгоритм я видел просто: "повторяем форму кривой с отступом d/2 по нормали пока нет касания другой части траектории. Как появляется -- уменьшаем вплоть до dmin/2 или 0". "другая часть - это массив из безье-фрагментов, несвязанных, насколько я понимаю, друг с другом".
С контуром, который обходим мы строим offset, т.е. нормаль+d/2 в каждой точке, а со всеми остальными фрагментами достаточно только факт пересечения проверять =>итеративно диаметр до нуля снижать.
P.S. Я немного замучился с запуском gcode_tools.py. Он умеет ругаться что не находит self.header и self.footer. Хотя они, вроде, явно прописаны. Может такое быть что они когда-нибудь (при каких-нибудь условиях) не инициализируются? в тех строках где они используются, я потёр обращения к ним и всё заработало.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 17:58
dormouse
Чем дольше смотрю, тем больше начинает казаться, что стоит отрастрировать синюю траекторию и вместо решения полноценной системы уравнений идти по векторной линии OB, строить от неё нормали, на ней для каждой точки в пределах до dmax/2 ищу "попал ли хоть один синий пиксель в этот диаметр" =)
Этакий комбинированный подход. В любом случае - для чисто растровой программы обязательно понадобится восстанавливать часть контура OB для построения нормали и т.п.
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 18:09
Nick
Прошу прощения, что не написал формулы в math.

dormouse писал(а):Надо будет немного освежить параметрические задания кривой.
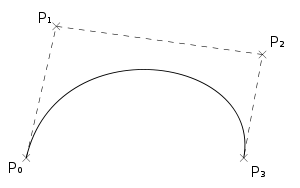
В инкскейпе все кривые задаются сегментами (между каждых двух контрольных точек), а сегменты кубическими кривыми безье:
задается двумя точками и касательными (с длинной) в них.
Картинка из википедии хорошо иллюстрирует построение кривой:
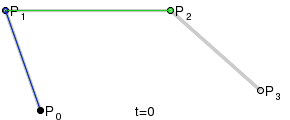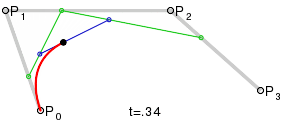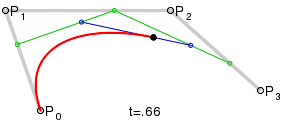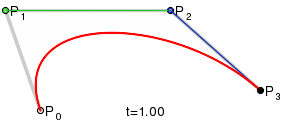
- Bezier_cubic_anim.gif (110.44 КБ) 7216 просмотров
http://ru.wikipedia.org/wiki/Кривая_Безье
Учитывая третью степень, если решение легко не выйдет
cubic solver я уже написал, когда вычислял пересечение прямой и кубической кривой безье. Но там 6-я степень

.
Собственно предлагается вместо поиска корней (если будет сложно) подставлять константы конкретного фрагмента и конкретной окружности и искать пересечение. Для ускорения можно BBOX'ы для начала проверить - может они разнесены в пространстве...
Я думаю нужно написать численной решение системы...
Что-то мне кажется странным - это решение системы надо прогнать для всех сегментов исходной "синей" кривой, т.е. фрагментами между каждыми точками из режима редактирования?
Да, придется, каждый сегмент - отдельная кривая безье.
Я забыл - во всех ли точках можно такую кривую разбить на отдельные сегменты, или они как-то связаны математически (вроде влияния "через один узел" на форму кривой)
Каждый сегмент просто бьется на два сегмента. А когда редактируешь узлы, если узел гладкий, то редактируются два сегмента.
Кстати пересечение окружности и кривой тоже решается только численно:
Окружность задается: x = r * cos(t), y = t * sin(t), либо квадратным уравнением, что в итоге дает уравнение 6-й степени => может быть до 6 точек пересечения

.
(прошу прощения, что не написал в math - эти формулы простые)
P.S. Я немного замучился с запуском gcode_tools.py. Он умеет ругаться что не находит self.header и self.footer. Хотя они, вроде, явно прописаны. Может такое быть что они когда-нибудь (при каких-нибудь условиях) не инициализируются? в тех строках где они используются, я потёр обращения к ним и всё заработало.
Эээээ... А что конкретно писал? На какую строчку ругался?
header и footer можно прописать в отдельных файлах и тогда скрипт их возьмет. Но у меня оба способа работают как надо...
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 18:25
dormouse
спасибо за разъяснения по Inkscape.
попробуйте на чистой winxp попробовать распаковать свой скрипт и натравить его на что-нибудь. Он умеет ругаться что self.footer/header не определён вообще. Насчёт подкладывания внешнего файла не пробовал, а вырезание самого обращения точно помогает. После попробую более детальные изыски.
Что порешим насчёт "не касания безье и окружности" ? (надо, кстати, очень строго подходить к вопросу - вдруг окружность пройдёт точно по точке начала и конца сегмента безье? тогда она может дать ложный диаметр! =) )
Можно ли в Inkscape скриптами сделать растрирование и комбинированную работу? Так же можно просто накидать равномерно N точек на кривую и про саму кривую вовсе забыть ? Получится обычная задача R^2 < x^2 + y^2 + z^2 для каждой такой точки {x,y,z}
Точнее R^2 < (x_i - x_r)^2 + (y_i - y_r)^2 + (z_i - z_r)^2
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 18:37
Nick
dormouse писал(а):Чем дольше смотрю, тем больше начинает казаться, что стоит отрастрировать синюю траекторию и вместо решения полноценной системы уравнений идти по векторной линии OB, строить от неё нормали, на ней для каждой точки в пределах до dmax/2 ищу "попал ли хоть один синий пиксель в этот диаметр" =)
Этакий комбинированный подход. В любом случае - для чисто растровой программы обязательно понадобится восстанавливать часть контура OB для построения нормали и т.п.
Не сцать!

Сейчас все решим, я уже нашел статейку в википедии!
http://en.wikipedia.org/wiki/Numerical_ ... _equations
и
http://en.wikipedia.org/wiki/Root-finding_algorithm
Еще условие добавилось: t3 от 0 до 1
Код: Выделить всё
alignl {
left lbrace alignl stack{
x = x_1+t_1 dx#y = y_1+t_1 dy
} right none
} newline newline
alignl {
left lbrace alignl stack{
x = x_2+t_2 dx_2#
y = y_2+t_2 dy_2#
dx_2 = 3ax t_{3}^2 + 2bx t_3 +cx#
dy_2 = 3ay t_{3}^2 + 2by t_3 +cy
} right none
}newline newline
alignl {
(B1_x - x)^2 + (B1_y - y)^2 = (ax t_{3}^3 + bx t_{3}^2 + cx t_{3} + ex - x)^2+(ay t_{3}^3 + by t_{3}^2 + cy t_3 + ey - y)^2
} newline newline
alignl {
t_3 in [0;1]
}
Re: Inkscape plug-in для экспорта в Gcode
Добавлено: 02 мар 2010, 18:42
Nick
dormouse писал(а):
(надо, кстати, очень строго подходить к вопросу - вдруг окружность пройдёт точно по точке начала и конца сегмента безье? тогда она может дать ложный диаметр! =) )
Точно, нужно будет не забыть замерить расстояния до концов сегментов.
Можно ли в Inkscape скриптами сделать растрирование и комбинированную работу? Так же можно просто накидать равномерно N точек на кривую и про саму кривую вовсе забыть ? Получится обычная задача R^2 < x^2 + y^2 + z^2 для каждой такой точки {x,y,z}
Точнее R^2 < (x_i - x_r)^2 + (y_i - y_r)^2 + (z_i - z_r)^2
Можно но проще Alt+b - это внутренний алгоритм инкскейпа. Иначе придется описывать всю отрисовку вручную. Из скриптов нет доступа ко внутренним функциям, они просто берут svg целиком, перерабатывают его как надо и отдают обратно inkscapе'у
Вот еще русская статейка как решить систему:
http://www.nsu.ru/matlab/Exponenta_RU/e ... oc.asp.htm
Сейчас домой приеду буду производные искать

.
